Etude du Code Secret de la Bible - Analyse détaillée
Mesurer la découverte du deuxième mot
Nous avons vu entièrement comment estimer l'espérance d'apparition d'un mot dans le texte biblique. Seulement, les prophéties réalisées dans le livre "Le Code Secret de la Bible" vont beaucoup plus loin que cela.
On peut trouver de nombreux tableaux où plusieurs mots se croisent. Ces mots sont souvent très proches l'un de l'autre, et leurs sens combinés produisent des idées étonnantes parfois. Il faudra estimer mathématiquement ce genre de phénomène. Il faut ainsi construire un modèle mathématique qui permette de mesurer l'apparition de plusieurs mots simultanément dans un tableau. Autant la conception du modèle précédent était simple, autant le choix du modèle adapté à cette nouvelle situation est plus compliqué. Nous allons voir qu'il y a plusieurs façons d'appréhender le problème. Pour faire le bon choix, il faut être lucide et le plus objectif possible.
Ce que nous cherchons, c'est l'espérance mathématique de l'apparition d'un tableau qui rapproche deux mots. Nous voulons savoir si tel tableau est surprenant ou non. Or il n'y a rien de plus subjectif que le fait d'être ou non surprenant. Comment mesurer cela ? Quand est-ce qu'un tableau est surprenant ? Quand est-ce qu'il ne l'est pas ? On peut aussi se demander quand est-ce qu'un tableau est plus surprenant qu'un autre. Il faudra choisir des critères, un moyen précis pour comparer et mesurer les tableaux.
Pour mesurer, il faut poser un critère, un étalon. Or quel critère peut nous affirmer qu'un tableau est impressionnant et qu'un autre ne l'est pas. Nous verrons que de nombreux choix sont possibles. Certains modèles donneraient des résultats mathématiques assez ahurissants. Si l'on choisissait comme modèle l'obligation de trouver les mots à une position précise, alors on obtiendrait des résultats infiniment petits, pratiquement impossibles. Par exemple, un mot de 5 lettres trouvé à la 12 358 ème position avec un code de 17, posséderait un espérance d'apparition de 1 chance sur 537 824 ; c'est infinitésimal. Un tel modèle est clairement inadapté. Car si l'espérance de trouver un mot à une place précise est très faible, l'espérance de trouver le même mot n'importe où dans le texte n'est pas faible du tout, elle est même souvent très élevée.
Quel est le bon modèle ? Cette question n'a pas de réponse indiscutable. Il est donc important d'être le plus objectif possible afin d'obtenir des résultats qui soient le reflet d'un choix lucide et impartial.
Le critère qui mesurera l'impression produite par un tableau utilisera la proximité des mots entre eux, car il est bien évident que plus le mot satellite est proche du mot principal et le croise, plus le tableau sera impressionnant. Il faudra donc pouvoir mesurer la proximité de deux mots. Mais nous verrons que cela n'est pas suffisant. Nous avons encore une série d'étape à suivre pour pouvoir estimer l'espérance d'un tableau de deux mots, et au fur et à mesure que nous avancerons nous expliquerons le choix que nous avons opéré pour mesurer "l'impression" d'un tableau.
Plan de la démarche pour le deuxième mot
Nous allons dresser le plan de la recherche permettant de mesurer un tableau à deux mots.
Nous désirons mesurer l'espérance d'un tableau qui présente deux mots. D'après le chapitre précédent nous savons déterminer l'espérance du mot principal (celui qui est le plus difficile à trouver dans le texte), il se peut que celui-ci ait une espérance de 15 comme de 0.01. Dans le premier cas cela signifie qu'on peut l'attendre probablement autour de 15 occurrences de ce mot, dans l'autre cas cela signifie qu'il y a peu de chances de le voir apparaître. En tout état de cause, il faut essayer de faire apparaître le mot satellite autour d'un des quelconques mots principaux trouvés. Il nous faut donc mesurer l'espérance de trouver le mot satellite à proximité d'un mot principal déjà connu. C'est ce qu'on appelle une espérance conditionnelle : "A la condition que le mot principal se trouve à telle position, l'espérance de trouver le mot satellite est de...". Voilà le travail qu'il nous reste à effectuer : supposons que nous ayons découvert une position et un saut de lettres tels qu'apparaît un mot principal, quelle est l'espérance de trouver le mot satellite à proximité de ce mot principal.
Pour mesurer l'espérance totale du tableau, il suffira de multiplier l'espérance du premier mot par l'espérance du second. En effet, si le mot principal a une espérance de 6, et que le mot satellite a une espérance de 3 ; cela signifie grossièrement que le mot principal apparaît 6 fois et que le mot satellite apparaît 3 fois autour de n'importe quel mot principal. La conclusion est simplement que l'on peut construire 18 tableaux différents car 6 x 3 = 18.
Pour pouvoir établir cette espérance conditionnelle, pour mesurer l'espérance de trouver un mot satellite à proximité d'un mot principal donné, nous allons suivre les 4 étapes suivantes :
1. La proximité de deux mots : nous avons vu que l'impression visuelle d'un tableau est très liée à la proximité des mots entre eux. Il faut donc construire une méthode qui permette de mesurer la distance des mots entre eux. Cela formera l'outil de base de notre travail.
2. Le nombre de positions dans un tableau fixé : nous avons vu dans le chapitre précédent - où l'on mesurait l'espérance d'un mot unique - que l'espérance découlait très rapidement du nombre de positions que peut prendre le mot principal. Il en est de même pour le mot satellite, son espérance est très étroitement liée au nombre de positions qu'il peut prendre. C'est ainsi qu'on va mesurer le nombre de positions que peut prendre un mot satellite à une proximité définie d'un mot principal dans un tableau fixé.
3. Le décompte des tableaux possibles : nous avons déjà vu, mais nous détaillerons à nouveau le fait qu'autour d'un mot principal donné il est possible de modifier un tableau par des glissements horizontaux ou verticaux. Cela permet de multiplier les chances de faire apparaître le mot satellite. Nous verrons quels sont tous les tableaux qui permettent de faire apparaître le mot satellite selon une "impressionnabilité" donnée. Et nous verrons comment les compter tous très exactement.
4. Le décompte des positions possibles : en disposant de tous les tableaux possible, on peut dénombrer toutes les positions possibles que peut prendre le mot satellite autour d'un unique mot principal. Seulement tous ces tableaux ont des positions qui se recoupent, il en résulte que le décompte des positions est loin d'être simple, mais il reste tout de même accessible.
Lorsque nous aurons effectué ces quatre étapes et que nous disposerons du nombre de positions possibles pour le mot satellite autour d'un mot principal donné au départ, il n'y aura qu'à déterminer son espérance par le même principe que pour le mot principal ; car c'est toujours le nombre de positions possibles que peut prendre un mot qui détermine quelle est son espérance.
La proximité de deux mots
Choix d'une mesure
Difficulté mathématique assez faible
Comment mesurer la distance entre deux mots ?
Dans un tableau où apparaît un mot principal et un mot satellite, nous désirons pouvoir mesurer la distance entre les deux mots ; or il y de nombreux choix possibles pour mesurer cette distance.
Le critère de mesure que nous choisissons est le suivant : la distance entre deux mots sera la plus petite distance entre le mot principal et la lettre la plus éloignée du mot satellite. Pour mieux comprendre, prenons un exemple de tableau :

Le mot 'second' est à la distance 7. 07 du mot 'principal' et le mot 'trois' est à la distance 7 du mot 'principal'.
Comment obtient-on cela ?
· Premièrement il faut comprendre que les mesures sont simplement établies en comptant les espaces entre deux lettres. L'unité de distance est l'espace entre deux lettres consécutive. Le mot 'trois' (qui est écrit à l'envers : 'siort') occupe une distance valant 4, c'est la distance qui sépare le 's' du 't' .
· Après avoir mesurer la distance entre les lettres, voyons comment mesurer la distance entre les mots. Prenons à nouveau le mot 'trois'. La lettre la plus éloignée du mot 'trois' au mot 'principal' est la lettre 't'. Quelle est la lettre du mot 'principal' la plus proche de ce 't' ? C'est la lettre 'l'. Ainsi, la plus courte distance entre le mot principal et la lettre la plus éloignée du mot satellite est 7, car il y a sept espaces entre le 't' et le 'l'. Ce cas là était le plus simple car la distance se calcule horizontalement en comptant les espaces.
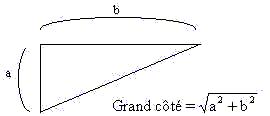
· Prenons l'autre cas, le mot 'second'. La lettre la plus éloignée du mot 'second' au mot 'principal' est la lettre 's'. Quelle est la lettre du mot 'principal' la plus proche de ce 's' ? C'est la lettre 'p'. Ainsi, la plus courte distance entre le mot principal et la lettre la plus éloignée du mot satellite est 7,07; pour calculer cela, il faut utiliser le théorème de Pythagore qui dit la chose suivante :
Lorsqu'on a un triangle avec un angle droit, alors la longueur du plus grand cotés se calcule à partir des petits cotés par la formule suivante :
Nous supposerons toujours que les tableaux sont à mailles carrées, c'est-à-dire que les distances entre deux lettres horizontales ou verticales sont les mêmes.
Ainsi toutes les distances se mesureront à partir des espaces qui sont entre les lettres.
Dans l'exemple précédent, calculons la distance entre les deux lettres 'p' et 's'. Plaçons-nous dans le triangle formé par les trois lettres 's', 'e', 'p'. Entre 's' et 'e' on trouve la distance 5; entre 'e' et 'p' on trouve aussi la distance 5. On obtient alors le résultat Racine(5²+5²)= 7,07, ce qui est le résultat annoncé.
Quels que soient le tableau de deux mots - un mot principal et un mot satellite - on peut calculer la distance qui les sépare à l'aide de cette méthode. Cela nous permettra de définir ce qui est psychologiquement impressionnant dans un tableau.
Pourquoi avons nous fait ce choix plutôt qu'un autre ? Tout simplement parce qu'il est permet de rendre compte de deux notions importantes :
· Cette mesure permet d'apprécier la distance qui sépare les deux mots, en utilisant la lettre du mot principal la plus proche du mot satellite.
· Elle permet aussi de mesurer la compacité des deux mots. En effet, la mesure s'adresse à la lettre la plus éloignée du mot satellite.
Exemple de mots identiquement distants
Difficulté mathématique assez faible
Plus cette distance est courte, plus le mot satellite est confiné près du mot principal ; et plus cette distance est longue, plus le second mot s'écarte du premier. C'est à partir de cette distance que nous allons estimer l'impression d'un tableau. Etait-ce le meilleur choix ? Je le crois, bien qu'il soit toujours discutable.
Voici quelques exemples de mots identiquement distants.
Premier tableau :

Deuxième tableau :
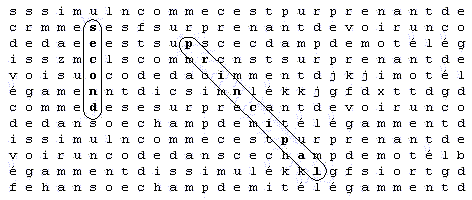
Troisième tableau :

Quatrième tableau :
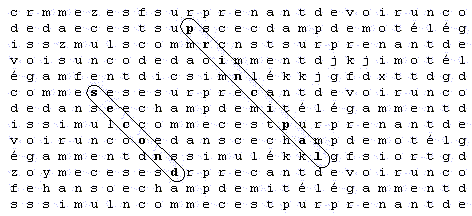
Ce qui compte c'est la distance du mot principal à la lettre la plus éloignée du mot satellite.
Il serait peut-être possible d'affiner cette distance en la rendant encore plus réaliste. Ce ne serait pas très difficile et il y aurait plein de méthodes possibles. Seulement, chaque méthode sera toujours discutable, car le critère "d'impressionnabilité" variera énormément d'un individu à l'autre.
Maintenant nous pouvons mesurer la distance entre deux mots. Nous pouvons entrevoir que c'est un critère intéressant pour mesurer l'impression d'un tableau, mais nous verrons plus loin, page *, comment l'utiliser.
Le nombre de position dans un tableau fixé
Une difficulté d'exactitude
Difficulté mathématique raisonnable
Maintenant que nous savons mesurer la distance entre deux mots, nous allons tenter de comprendre comment mesurer l'espérance de trouver un mot satellite près d'un mot principal fixé. Avançons un petit peu dans le problème. Depuis le début de notre recherche pour le deuxième mot, nous avons supposer connaître la position du mot principal, par exemple la 125ème position. avec un code 32. Et bien supposons de plus maintenant qu'on dispose aussi d'un tableau où l'on peut voir apparaître ce mot. Nous dirons dans ce cas que le mot principal est fixé dans un tableau. Comme c'est le cas dans le tableau ci-après, par exemple. Nous verrons plus loin que le même mot principal peut être fixé (ou peut apparaître) dans plusieurs tableau. Nous supposons donc que le mot principal est dans un tableau particulier que fixé. Nous nous intéressons à découvrir le mot satellite dans ce tableau particulier qui a été fixé.
Le mot satellite peut-il apparaître à proximité du mot principal dans notre tableau ? Peut-il apparaître à une proximité que nous choisissons ? Il faudra pour cela commencer par savoir choisir une proximité. Maintenant que nous avons vu la distance séparant deux mots, cela est très simple. Dire que le mot satellite apparaisse à une proximité de 3 signifiera que la distance entre le mot principal et le mot satellite sera au pire 3 ; c'est à dire 3 ou moins. Regardons l'exemple ci-après : dire que le mot satellite apparaît une distance inférieure à 3 (ou à une proximité de 3) du mot principal revient tout simplement à dire que le mot apparaît à l'intérieur du trait en pointillé.
Il nous reste maintenant la plus grande part du travail : comment mesurer l'espérance que le mot satellite apparaisse à une proximité donnée d'un mot principal ?
Afin de rendre les explications plus faciles, étudions un exemple : à l'intérieur du tableau suivant, quelle est l'espérance de voir apparaître le mot 'deux' à une distance inférieure ou égale à 3 du mot 'premier'.

Si nous observons bien, nous nous apercevons que le mot 'deux' n'est pas présent à une distance inférieure ou égale à 3 du mot 'premier', mais cela ne nous empêche nullement de nous intéresser quand même à la question suivante : quelle est l'espérance de le voir apparaître dans un tel tableau à une distance inférieure ou égale à 3 ? En répondant à cette question, nous pourrons affirmer s'il est naturel ou non que le mot "deux" n'apparaisse pas ici. Comment procéder mathématiquement pour obtenir la réponse à une telle question ?
La question se décompose en plusieurs étapes :
1- Tout d'abord : quelles sont les lettres qui sont à une distance inférieure à 3 du mot 'premier' ?
2 - Puis quel est le nombre de positions que pourrait prendre le mot 'deux' à l'intérieur de l'ensemble de ces lettres ?
3 - La dernière étape serait : comment généraliser un tel procédé ?
Voici une ébauche sommaire de la réponse à ces questions :
· Pour répondre à la première question, la méthode la plus simple serait de calculer, pour chaque lettre, la distance qui la sépare du mot 'premier'. Mais ce travail serait très long et pénible. Une autre méthode consiste à tracer la limite qui correspond à la distance 3 comme nous l'avons fait sur l'exemple ci-dessus. Cette limite a la forme d'un rectangle terminé par deux demi-disques, ou plus simplement la forme d'un stade. Nous appellerons cette forme la surface de recherche. Il suffit ensuite de compter les lettres à l'intérieur de cette forme. On peut s'apercevoir que certaines lettres (comme le 'T' par exemple mis en gras en bas de la surface de recherche) peuvent poser une ambiguïté. Une bonne méthode consisterait à compter premièrement toutes les lettres qui sont assurément dans la surface de recherche, puis à faire le calcul uniquement pour constater si les lettres ambiguës sont ou non dans la surface. Par cette méthode, nous pouvons compter 83 lettres dans notre exemple.
· On peut maintenant essayer de répondre à la deuxième question. A partir des 83 lettres trouvées, combien peut-on construire de positions pour les 4 lettres du mot 'deux'? Rappelons-nous qu'une position pour un mot de 4 lettres, est tout simplement une suite de 4 lettres alignées et régulièrement espacées. On s'aperçoit que pour déterminer les positions possibles pour un mot, la nature des lettres n'a aucune importance ; la seule chose qui compte, c'est le nombre de lettres du mot. Ici, nous cherchons toutes les positions possibles pour un mot de 4 lettres. Pour dénombrer toutes les positions possibles, nous proposons de décomposer le travail de la façon suivante :
- Commençons par choisir une lettre parmi les 83 qui sont présentes. Nous allons compter toutes les positions possibles que peut prendre un mot de quatre lettres commençant par cette lettre que nous avons choisie.
- Il suffit alors de déterminer le nombre de façons dont on peut disposer les 3 autres lettres régulièrement.
- En dernier lieu on reproduit ces deux étapes pour chaque première lettre possible.
Ce qui donne pour l'exemple ci-dessus :
- Prenons par exemple la lettre 'i' (elle est placée en haut à gauche, elle est mise en gras). Comptons combien de positions pour un mot de quatre lettres il est possible de construire à partir de ce 'i', en supposant que cette lettre est la première lettre du mot.
- Pour cela il faut essayer toutes les lettres qui entourent le 'i' en vérifiant si elles peuvent être une deuxième lettre du mot. Par exemple si l'on choisit le 'c' à droite du 'i', on s'aperçoit que c'est une deuxième lettre possible car, en respectant le même espacement, la troisième lettre (le 's') et la quatrième lettre (le 'i') du mot seraient bien inscrites dans la surface de recherche. Le 's' en dessous du 'i' convient aussi. Mais par contre le 'd' en haut à droite n'est pas une deuxième lettre possible car, en respectant le même espacement, la troisième lettre (le 'a') et la quatrième lettre (le 'r') ne seraient pas inscrites dans la surface de recherche. Si on fait le compte total des secondes lettres possibles, on en trouve seulement 9 ; c'est-à-dire qu'il y a seulement 9 positions possibles pour un mot de 4 lettres à partir de ce 'i'.
- Enfin il faut refaire ce compte pour chacune des 83 lettres de la surface, ce qui est plutôt fastidieux. Si on avait à faire à une surface de recherche encore beaucoup plus grande, on peut imaginer combien le travail serait long.
· Alors, dernière étape, comment généraliser un tel procédé ? C'est plutôt difficile. Mathématiquement s'il fallait déterminer le compte exact du nombre de positions, la réponse serait plutôt compliquée. Pour un mot principal donné et une distance donnée dans un tableau, il n'y a pas de formule simple qui détermine le nombre exact de positions que peut prendre un mot satellite.
En fait, il est possible de procéder à une petite simplification du problème qui, sans altérer la qualité des résultats, donnera une estimation très satisfaisante du nombre de positions. Il est même possible de calculer dans quelle mesure le résultat est altéré ; et nous pourrions constater que cette altération est négligeable dans l'ensemble des cas que nous traiterons.
Une bonne estimation
Difficulté mathématique raisonnable
Nous allons donc procéder à la simplification du problème. Cette estimation se fait en assimilant les lettres à des formes géométriques : on ne suppose plus qu'on a à faire à un tableau de lettres mais à une surface ; les lettres sont assimilées à des points et le mot principal est comme un trait supportant ces points. Voici un schéma qui représente tout cela :
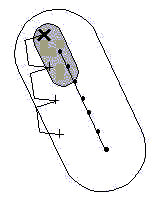
Si l'on choisit une lettre parmi les 83 pour être la première lettre d'une position d'un mot de quatre lettres, cela revient à choisir un point à l'intérieur de la surface de recherche : sur l'exemple ci-dessus nous avons choisi comme première lettre le point représenté par la croix épaisse ( X ). Nous cherchons à connaître le nombre de positions possibles pour un mot de quatre lettres dont la première lettre est cette croix.
Toute l'astuce réside dans le fait suivant. Nous disposons de la première lettre du mot représentée par la croix et il suffit de rechercher géométriquement quelles sont les deuxièmes lettres possibles. En effet lorsqu'une deuxième lettre est choisie, tout le mot est défini : il suffit de placer les lettres suivantes selon le même espacement. Le mot convient lorsque la dernière lettre est toujours inscrite à l'intérieur de la surface de recherche. On en déduit que les différentes positions possibles sont exactement celles dont la deuxième lettre est inscrite dans une forme identique à la surface de recherche, mais ayant une taille trois fois plus petite (c'est la forme qui est dessinée en gris). Nous appellerons cette petite forme grisée : la surface locale.
Détaillons un petit peu comment nous obtenons cette surface locale. Dans un mot de quatre lettres, il y a trois espaces. Si la deuxième lettre du mot est inscrite dans la forme grise, alors en prolongeant trois fois la même distance (comme cela est représenté sur le dessin ci-dessus), on obtient forcément que la quatrième lettre est à l'intérieur de la grande forme. Cela fonctionne bien car la surface locale est placée de façon à ce que la surface de recherche soit un agrandissement (une homothétie) de la surface locale. Le centre de l'agrandissement est exactement la première lettre du mot. Le rapport de l'agrandissement est 3 ; c'est le nombre d'espaces entre les lettres du mot. De cette façon, on peut visualiser le nombre exact de position qu'on peut construire en prenant n'importe quelle lettre comme première lettre du mot.
Jusque là le raisonnement est exact, nous n'avons pas encore fait d'estimation. L'estimation aura lieu lorsque nous allons évaluer le nombre de lettres à l'intérieur de la surface locale ou à l'intérieur de la surface de recherche.
Nous allons tout simplement dire que le nombre de lettres est correctement estimé par la surface de la forme concernée. En effet, si les lettres sont placées dans un tableau séparées d'un centimètre les unes des autres, on peut constater qu'il y a une lettre par cm². De cette façon, compter la surface d'une forme ou bien les lettres qu'elle contient revient environ au même. Cette estimation est une très bonne méthode simplificatrice, car les lettres sont réparties de façon uniforme dans toutes les surfaces que nous étudierons.
L'intérêt de cette méthode est de remplacer le décompte laborieux des lettres par un calcul de surface beaucoup plus élémentaire. La forme qui nous concerne présentement (voir figure ci-dessous) est relativement simple. Quel que soit le mot étudier, elle se décompose en trois parties : un rectangle et deux demi-disques qu'on peut voir ci-dessous.
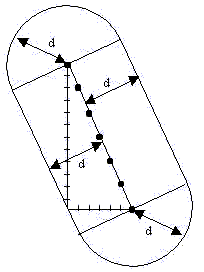
· Le rectangle a pour longueur exactement la taille qu'occupe le mot principal. Si le mot principal était vertical, il se trouverait que cette taille serait le nombre de lettres du mot moins 1 (car il y a toujours un espace de moins qu'il n'y a de noeuds à une corde). Quand le mot principal est penché et qu'il y a des sauts de lignes entre ses lettres consécutives, il faut calculer cette distance. Voici un exemple pour nous donner de comprendre les calculs à faire. Dans le dessin ci-dessous le mot principal est fait de 7 lettres. Il est penché et il apparaît avec un saut de ligne entre chaque lettre.
La longueur du rectangle se calcule par la formule de Pythagore que nous avons déjà utilisée. La longueur est de Racine(6² + 12²)=13.41. Pour obtenir ce calcul, il suffit de compter horizontalement et verticalement le nombre de lettres qui séparent la première lettre du mot de la dernière : c'est ce que nous avons représenté par les graduations.
Si l'on appelle d la distance jusqu'à laquelle on effectue la recherche du mot satellite, alors la largeur du rectangle est 2d. On trouve la surface du rectangle par la formule : surface = largeur ´ longueur
· Pour les demi-cercles le rayon est d, donc la surface est donnée par la formule d'un demi-disque : Pi . d² / 2
.Avec ces résultats nous pouvons calculer la surface totale de la forme étudiée : si l'on appelle L la longueur qu'occupe le mot principal et d la distance de recherche, alors la surface de la figure est exactement : L. 2d + Pi.d². Cette formule permet d'évaluer le nombre de lettres contenues dans cette surface.
Si l'on essaie d'appliquer cette formule à l'exemple initial (cf. le tableau du chapitre : une difficulté d'exactitude) pour calculer le nombre de lettres qui sont à une distance inférieure à 3 du mot 'premier', on trouve Racine(6²+6²) x 2 x 3 + Pi x 3² = 79.2. Or en comptant nous en avions trouvé 83. Nous constatons que l'estimation est tout à fait honorable, surtout qu'il s'agit d'une petit surface de recherche ; en effet, plus la surface de recherche est grande, plus l'estimation sera exacte.
Si l'on essaie de critiquer cette méthode d'estimation, on peut trouver des cas où l'estimation n'est pas tout à fait bonne. Par exemple les tableaux où le mot principal apparaît verticalement et où la distance de recherche est proche d'un nombre entier sont les cas où l'estimation est la moins bonne. Mais cela n'a pas trop d'importance car, quoi qu'il en soit, dans tous les cas que nous utiliserons c'est une estimation qui reflétera bien l'ordre de grandeur ; et dans la plupart des cas l'estimation sera même très précise.
Le nombre de positions possibles pour le mot satellite
Difficulté mathématique moyenne
Essayons maintenant de déterminer précisément le nombre de positions possibles pour un mot satellite. Selon la méthode que nous avons décrite, choisissons une lettre quelconque parmi les lettres de la surface de recherche. Nous désirons déterminer le nombre de positions possibles pour un mot satellite de q lettres dont la première lettre est celle que nous venons de choisir. Essayons de construire la formule mathématique qui répond à cette question.
Nous avons vu que le nombre de positions possibles correspond au nombre de lettres inscrites dans la surface locale. Sur le nombre de lettres présentes dans la surface locale, il faudra tout de même en retrancher une, car la lettre initiale du mot n'est pas une deuxième lettre possible ; il ne faut donc pas la compter.
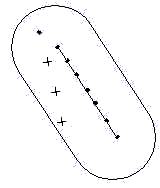
Prenons un exemple : Si le mot principal de 7 lettres occupe une distance de 10.5 ( L = 10.5 ), si la distance à laquelle on cherche est 3.5 ( d = 3.5 ) et si le mot satellite recherché possède quatre lettres ( q = 4 ), alors selon la formule que nous avons établie le nombre de lettres dans la grande forme est environ :
10.5 x 2 x 3.5 + Pi x 3.5² =111.98, soit 112 lettres.
Comme le second mot possède 4 lettres, il y a 3 espaces entre ses lettres. Comme nous l'avons vu, le nombre de secondes lettres se détermine facilement par la taille de la surface locale :
10,5/3 x 2 x 3,5/3 + Pi. (3,5/3)² = 12.44 auquel il faut retirer 1.
Cela signifie qu'en moyenne il y a 11.44 positions possibles pour cette première lettre. On recommence l'opération pour chaque lettre pouvant être la première du mot satellite, c'est-à-dire pour toutes les lettres de la surface de recherche. On s'aperçoit qu'on fait exactement le même calcul pour toutes les lettres. Le nombre total de positions est donc donné par le produit du nombre de lettres de la surface de recherche multiplié par le nombre de positions possibles dans la surface locale. C'est donc le produit des deux valeurs que nous venons de calculer :
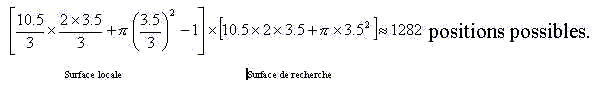
C'est le résultat qu'on cherchait.
Ce calcul se généralise pour une situation quelconque. Prenons :
- L la longueur qu'occupe un mot principal,
- q le nombre de lettre d'un mot satellite,
- d une distance de recherche,
alors le nombre de positions possibles où l'on peut trouver le mot satellite situé à une distance inférieure à d du mot principal se détermine par la formule suivante :
qui se simplifie pour donner la formule finale suivante :
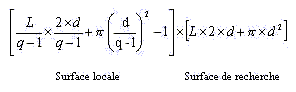
Le nombre de positions possibles pour trouver un mot satellite à proximité d'un mot principal dans un tableau donné est estimé par :
nombre
de positions =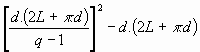
Où :
- d est la distance de recherche
- q est le nombre de lettres du mot satellite
- L est la taille qu'occupe le mot principal.
(l'unité étant la distance entre deux lettres consécutives)
Par ce procédé, on peut calculer le nombre de positions d'un mot satellite à proximité d'un mot principal dans n'importe quel tableau où l'on voit apparaître le mot principal.
Ensuite, il suffit de se rappeler que lorsqu'on connaît l'espérance d'apparition d'un mot et le nombre de positions possibles, alors le produit de ces deux nombres donne l'espérance de voir apparaître ce mot. En calculant l'espérance du mot satellite à partir de ses lettres comme nous l'avons déjà vu et en calculant le nombre de positions possibles à partir de la formule que nous venons d'établir, nous pouvons connaître l'espérance de faire apparaître le mot satellite à proximité du mot principal à l'intérieur de n'importe quel tableau donné.
Les différents tableaux possibles
Difficulté mathématique raisonnable
Nous avons obtenu le résultat que nous cherchions. Mais ce résultat nous donne l'espérance d'un mot satellite à l'intérieur d'un seul tableau. Or dans un même texte de 305 000 lettres, le même mot principal peut apparaître dans un très grand nombre de tableaux différents, dans chacun desquels pourra apparaître le mot satellite
Il faut donc commencer par faire le compte des différents tableaux possibles. Ce travail n'est pas extrêmement compliqué. Il n'y a que deux façons de faire apparaître différents tableaux autour du même mot principal :
· Soit en écartant verticalement les lettres du mot principal, c'est-à-dire en sautant des lignes intermédiaires.
· Soit en écartant horizontalement les lettres du mot principal, c'est-à-dire en faisant glisser chaque ligne de quelques lettres.
Revoyons brièvement ces méthodes en fixant une terminologie appropriée :
Les glissements verticaux (ou les sauts de lignes).
Lorsqu'on a trouvé un mot à l'intérieur d'un texte par le procédé du saut de lettres, il est toujours possible de le faire apparaître verticalement dans un tableau. Pour cela il suffit de construire un tableau ayant comme largeur la taille du code (c'est-à-dire le nombre du saut de lettre) dans lequel on a trouvé le mot. Si par exemple on a trouvé le mot 'premier' dans un code 5040, il suffit de construire un tableau de 5040 lettres de large et le mot 'premier' apparaîtra alors verticalement. Evidemment nous ne présentons pas les 5040 lettres qui forment chaque ligne, mais uniquement les lettres qui sont autour du mot.
Voici le tableau :

Il faut comprendre qu'il est possible de construire d'autres tableaux en utilisant le même mot principal. Par exemple, il suffit de construire un tableau de largeur 2520 (qui est la moitié du précédent). On obtient alors un nouveau tableau où le mot 'premier' apparaît toutes les deux lignes.
Voici le même mot mais dans un tableau de 2520 lettres de large (on ne représente évidemment pas toutes les lettres non plus) :

On dira dans ce cas qu'on a procédé à un glissement vertical de 2 lettres. Le tableau original correspond à un glissement vertical de 1 lettre, c'est-à-dire que les lettres sont consécutives.
En construisant un tableau de largeur 1680, on obtiendrait le même mot avec cette fois-ci un glissement vertical de 3 lettres, etc_
Ce procédé du glissement vertical apporte beaucoup de positions supplémentaires lorsqu'on cherche à faire apparaître un mot satellite auprès d'un mot principal donné. En effet toutes les lignes intermédiaires apportent des lettres nouvelles et chaque lettre nouvelle permet beaucoup de combinaisons supplémentaires possibles.
Les glissements horizontaux (ou les décalages de lignes).
En reprenant l'exemple précédent, nous allons voir qu'il est possible d'effectuer aussi des décalages horizontaux. Reprenons notre tableau de 5040 lettres de large :
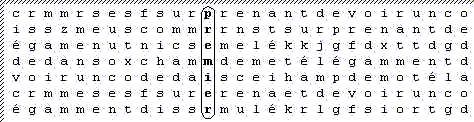
En construisant le même tableau avec cette fois-ci 5041 lettres de large, on obtiendrait le tableau suivant :
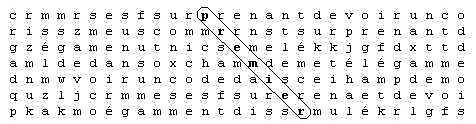
On dira qu'on a construit un tableau avec un glissement horizontal de 1 lettre. Le tableau d'origine ne contient évidemment aucun glissement horizontal. On pourrait aussi construire un tableau de 5039 lettres de large qui sera aussi un tableau avec un glissement horizontal de 1, mais cette foi-ci dans l'autre inclinaison. Le tableau de 5042 lettres de large ferait apparaître le mot 'premier' avec un glissement horizontal de 2. Etc...
Comme nous l'avons vu, la technique du glissement horizontal permet de rapprocher certains mots satellites. Un tableau avec des glissements horizontaux permet aussi la fabrication de quelques positions supplémentaires.
Comment mesurer "l'impressionnabilité" d'un tableau ?
Rappelons-nous la question qui nous intéresse : quelle est l'espérance de voir apparaître un mot satellite donné à proximité d'un mot principal donné ? Pour pouvoir répondre à cette question, il faut commencer par répondre à celle-ci : lorsqu'on désire estimer un tableau où apparaissent un mot principal et un mot satellite, quels sont tous les autres tableaux qui lui sont équivalents ? (Nous appelons tableaux équivalents, des tableaux contenant les mêmes mots qui ont la même impression).
En effet, lorsqu'on ne se limite pas à chercher autour d'un mot principal dont la position est fixée, mais qu'on s'autorise la recherche dans tous les tableaux équivalents, les chances de trouver le mot satellite augmentent considérablement. Il faut poser un critère de comparaison qui donne une échelle de comparaison, un critère mesurant l'impression que procure un tableau.
Les problèmes se résolvent lorsqu'on se pose les bonnes questions. La bonne question à se poser ici est la suivante : en considérant deux tableaux différents contenant le même mot 'premier', où placer le mot satellite dans chacun des tableaux pour que ces deux tableaux offrent la même impression visuelle ? La question peut se résumer à : comment définir mathématiquement "la même impression" ?
La question n'est pas très simple, il suffit de faire la constatation suivante : nous avons étudié la distance de recherche (page *), ce qui nous a permis d'estimer l'impression d'un tableau en fonction de la distance du mot satellite auprès d'un mot principal fixé. Mais lorsqu'on s'intéresse à des tableaux différents autour du même mot principal qui peut être à des positions variables, la distance de recherche n'est plus un critère valable. Elle ne mesurerait pas correctement l'impression d'un tableau.
Dans les deux tableaux suivants le mot satellite est à la même distance de recherche :
Premier tableau :
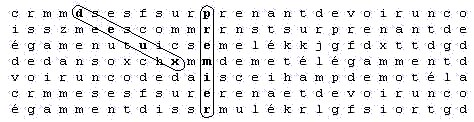
Deuxième tableau :

Dans chacun de ces tableaux, le mot satellite apparaît à la distance 8 du mot principal. Or il apparaît que le premier tableau est nettement plus impressionnant que le second où le mot 'premier' apparaît avec un glissement vertical de 2 lettres. C'est un exemple qui montre que la distance entre les mots n'est pas suffisante pour estimer l'impression d'un tableau.
L'espérance comme critère ?
La notion de distance du mot satellite au mot principal n'est pas suffisante pour exprimer "la même impression". On peut alors se demander si le critère le plus naturel n'est pas " l'espérance de trouver le mot satellite " ? En effet, plus l'espérance de trouver un mot satellite est petite, plus l'impression semble forte, non ? Deux tableaux ayant même espérance ont-ils même impression ? Et bien là encore, la réponse est non ! Ce n'est pas non plus un critère recevable. En effet, l'espérance est directement déterminée par le nombre de positions possibles pour le mot satellite ; et un tableau très allongé qui a le même nombre de positions qu'un tableau très compact (et donc la même espérance) n'est pourtant pas aussi impressionnant.
En voici un exemple : les deux tableaux suivants ont pratiquement la même espérance de voir apparaître le mot satellite 'deux' à proximité du mot principal 'premier':
Premier tableau :
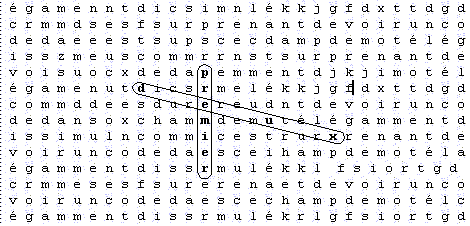
Et voici le second tableau :

Le second tableau, beaucoup plus étalé, est clairement moins impressionnant que le premier et pourtant _ l'espérance du second tableau est plus faible que celle du premier. Pour le constater, il suffit d'utiliser les formules que nous avons établies qui permettent de mesurer l'espérance d'un tableau.
L'espérance n'est donc pas un critère satisfaisant. Et cette constatation est importante, car en général l'usage naturel des mathématiques veut que l'impression d'un événement soit étroitement liée avec son espérance mathématique. Or les tableaux que nous étudions ne suivent pas cette règle intuitive. Ce critère donnerait des espérances beaucoup trop élevées par rapport à la réalité.
Il faut donc déterminer comment peut être mesurée l'impression visuelle d'un tableau _ et ce n'est pas très facile.
La compacité comme critère de comparaison ?
Difficulté mathématique raisonnable
Plusieurs critères de comparaison sont possibles, c'est pourquoi il faut être très lucide en faisant notre choix. Il ne faut pas choisir un critère qui forcera les résultats à notre avantage. Sur ce point, le choix de l'espérance comme critère aurait été très avantageux, il aurait produit des résultats très élevés pour les tableaux.
Il faut bien comprendre ce qui impressionne réellement dans un tableau. Il y a un élément que probablement tout le monde acceptera de prendre en compte : c'est la compacité du tableau. Un tableau très allongé, très étendu (dans une direction quelconque) est moins impressionnant qu'un tableau compact, ramassé ; même si ces derniers ont la même espérance, nous en avons vu un exemple dans le dernier chapitre. C'est un fait important de considérer la compacité sinon il serait possible d'augmenter considérablement l'espérance en autorisant des dizaines de glissements verticaux qui offriraient d'innombrables positions nouvelles.
L'impression d'un tableau est donnée par son aspect global : moins un tableau est étalé, plus il est ramassé, plus le tableau est impressionnant. Il serait alors logique d'utiliser la compacité comme critère de comparaison. La compacité peut se mesurer en calculant tout simplement la plus grande distance entre deux lettres des mots du tableau, plus courte est cette distance, plus grande est la compacité.
Mais le choix de la compacité - c'est-à-dire la distance maximale entre les lettres des mots - n'est pas un critère convenable. Voici un exemple qui montre que la compacité ne suffit pas à elle seule pour définir l'impression d'un tableau. Voici deux tableaux :
Premier tableau :
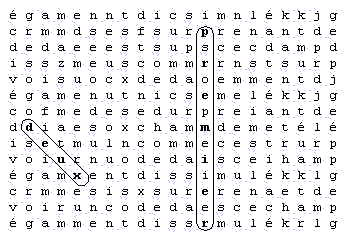
Deuxième tableau :
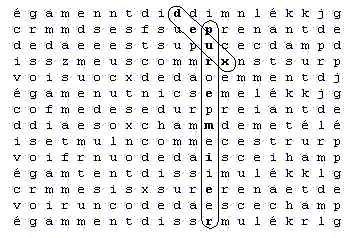
Si l'on observe ces deux tableaux, je pense que chacun s'entendra pour dire que le second est clairement plus impressionnant que le premier. Mais si l'on mesure la compacité, le premier tableau mesure 12.53. En effet, la compacité est la plus grande distance qu'on peut trouver entre deux lettres du tableau. Les lettres les plus éloignées sont le 'd' du mot 'deux' et le 'p' du mot 'premier' (le 'r' final du mot 'premier' conviendrait aussi) ; il suffit alors de mesurer la distance par le théorème de Pythagore et on trouve 12.53. Par la même méthode, on trouve que la compacité du second tableau est de 13.15. Ainsi, le second tableau, qui est le plus impressionnant, est pourtant le moins compact.
Cet exemple démontre que la compacité, à elle seule, ne suffit pas à définir l'impression de deux tableaux. En même temps que la compacité, la distance de recherche possède aussi un rôle d'impression psychologique, ce qui va nous conduire naturellement au choix développé dans le paragraphe suivant.
Le critère de comparaison des tableaux
Difficulté mathématique assez faible
Malgré la difficulté qui existe à enfermer l'impression psychologique "d'impressionnabilité", il faut faire un choix qui permettra de faire les calcul. Nous ne détaillerons pas à l'excès ce qui nous a conduit au choix suivant, mais disons qu'il est un compromis entre la juste impression psychique et la simplicité ; ce qui permet de ne pas trop s'étendre en débats insolubles.
Le choix qu'on fera pour définir l'impression d'un tableau est le suivant : deux tableaux contenant le même mot principal et le même mot satellite seront considérés comme identiquement impressionnants si les longueurs maximales de recherche sont les mêmes. Nous définissons précisément la longueur maximale de recherche par la valeur : L+2d, où L est la taille qu'occupe le mot principal et d la distance de recherche.
Cette valeur n'est pas dénuée de sens, elle correspond très exactement à la hauteur de la surface de recherche que nous avons souvent utilisée. Nous avons représenté cette surface de recherche en gris dans l'exemple qui suit. Dans cet exemple, en constatant que la distance de recherche est 4 et que le mot occupe une taille de 5-1, on peut trouver la longueur maximale de recherche par le calcul suivant (5-1) + 2 x 4 = 12.

Il faudra bien retenir ce critère permettant de comparer les tableaux entre eux : on dira que deux tableaux contenant les mêmes mots seront identiquement impressionnants si la longueur maximale de recherche est la même ; un des deux tableaux sera plus impressionnant que l'autre si sa longueur maximale de recherche est inférieure. Plus la longueur maximale de recherche est petite, plus le tableau est impressionnant. Cela revient à dire que l'impression d'un tableau provient de la hauteur de la surface de recherche. L'intérêt de ce critère est qu'il prend en compte en même temps la compacité et la proximité des mots.
Exemple de tableaux équivalents
Voici trois exemples de tableaux ayant pratiquement la même longueur maximale de recherche. Suivant notre modèle ces deux tableaux sont donc identiquement impressionnants car L+2d est pratiquement constant dans les trois cas. Ce choix semble à peu près convenable, même s'il est toujours discutable. Observons l'effet rendu :
Premier tableau :

Deuxième tableau :

Voici encore un troisième tableau qui a pratiquement la même longueur maximale de recherche, donc pratiquement la même impression :

Il est bien évident que nous ne pourrons pas établir un modèle complètement satisfaisant pour définir l'impression d'un tableau. En effet, notre choix présente aussi quelques désavantages. La beauté d'un tableau dépend beaucoup de l'impression psychologique perçue par chacun. On pourrait toujours ajouter d'autres facteurs qui interviennent dans la perception du tableau. Mais l'intérêt de notre choix est un équilibre entre la simplicité et le nombre des facteurs qui interviennent ; en augmentant le nombre de facteurs, on risquerait de produire des désaccords. De toute façon même si notre choix n'était pas le meilleur, un autre choix lucide devrait être quantitativement à peu près équivalent et produire, à la fin, des résultats mathématiques à peu près semblables.
Les decomptes des tableaux possibles
Résumé global de la démarche
Difficulté mathématique raisonnable
Maintenant que nous avons vu comment estimer l'impression des différents tableaux, revenons à notre question initiale : lorsque nous sommes devant un tableau comportant un mot principal et un mot satellite, nous désirons en déterminer l'espérance. Il faut bien comprendre le point suivant : il ne suffit pas de calculer l'espérance du tableau considérer, il faut calculer l'espérance de trouver n'importe quel tableau équivalent. Il faut estimer toutes les situations possibles où le mot principal et le mot satellite sont à la proximité recherché l'un de l'autre. En effet ce qui compte, lorsqu'on cherche à savoir si un des tableaux publiés par Drosnin est une conséquence naturelle du hasard ou non, ce n'est pas de savoir si précisément le tableau publié peut être trouvé, mais c'est de savoir si l'on peut trouver un tableau contenant les mêmes mots qui ait la même impression, quelle que soit sa position a priori.
C'est ainsi que pour étudier l'espérance d'un tableau, il faut comptabiliser tous les tableaux vérifiant les conditions suivantes :
· Ils contiennent les deux mots du tableau étudié.
· Ils possèdent une espérance au moins aussi grand que le tableau étudié.
A partir de ces tableaux, il sera possible de compter toutes les configurations différentes où les deux mots étudiés peuvent apparaître à proximités l'un de l'autre.
Afin d'y voir clair, résumons notre démarche depuis le départ; elle se passe en trois temps :
· Il faut commencer par estimer tous les mots principaux possibles. Cela nous savons le faire d'après les formules que nous avons établies dans les pages précédentes.
· Il faut ensuite savoir, à partir de chaque mot principal, combien de tableaux différents on peut construire. Et pour cela, nous avons vu que les deux grands principes donnant lieu à de nouveaux tableaux sont le glissement horizontal et le glissement vertical.
· Il faut ensuite estimer, à l'intérieur de tous ces tableaux, combien de positions distinctes, on peut trouver pour le mot satellite.
Nous en sommes à la deuxième étape ; il faudra établir, à partir d'un mot principal donné, quels sont tous les tableaux que nous pouvons construire ? Il suffit de procéder à des glissements verticaux et horizontaux. Mais une remarque possède toute son importance : il n'est pas possible de faire autant de glissements qu'on le veut, car la distance de recherche doit être constante. Or en procédant à des glissements, la taille du mot principal s'allonge et par voie de conséquence on dépasse très vite la longueur maximale de recherche. Il faudra prendre en compte tous ces paramètres qui ont un rôle dans les calculs. Nous verrons qu'il est possible, pour faire le décompte de tous les tableaux, d'utiliser une simplification.
Dans la troisième étape, pour calculer l'ensemble des positions possibles du mot satellite, il semblerait naturel de faire la somme des positions qu'on trouve dans chacun des tableaux comptabilisés à la deuxième étape. Mais la réalité n'est pas si simple ; certaines positions se trouvent dans plusieurs tableaux différents et il ne faut pas les compter deux fois. En voici un exemple : les deux tableaux suivants sont construits autour du même mot principal. Le premier tableau a comme largeur (réelle et non visible) la taille du code du mot principal (le nombre de lettres qu'il faut sauter pour trouver la lettre suivante), ce qui conduit à trouver ce mot positionné verticalement. Le second tableau a comme largeur la taille du code divisé par deux, ce qui conduit à un glissement vertical de 2 lettres (on dira dans le premier tableau qu'il y a un glissement vertical d'une lettre). Dans ces deux tableaux, on peut constater qu'il existe une position où l'on retrouve le même mot 'deux' ; dans chacun des tableaux, ce mot est fait avec exactement les mêmes lettres du texte de départ. La présentation du mot est différente uniquement parce que la largeur de tableau qu'on a choisie est différente.
Premier tableau :

Dans le second tableau où l'on a un glissement de 2 lettres, on retrouve aussi exactement le même mot 'deux' qui n'a pas disparu :
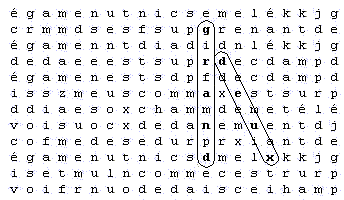
Ainsi pour calculer le nombre total de positions présentes dans tous les tableaux, il n'est pas possible d'ajouter séparément les positions de chaque tableau, sinon certaines positions seraient comptées plusieurs fois.
Après avoir dressé un aperçu du travail qui nous reste à faire, revenons-en à la deuxième étape de notre recherche : compter tous les tableaux équivalents autour d'un même mot principal.
Une simplification
Difficulté mathématique raisonnable
Comment s'y prendre ? Si l'on voulait être très précis dans les comptes des tableaux, le travail se compliquerait énormément. C'est la raison pour laquelle nous allons procéder à nouveau à des petites simplifications : nous ne compterons pas toutes les positions possibles, nous en compterons un peu moins. Les résultats que nous obtiendrons seront donc un peu sous évalués. Ce n'est pas grave car nous voulons montrer que les tableaux proposés dans le livre de Drosnin sont tout à fait probables, qu'ils n'ont rien d'exceptionnels. Si les résultats que nous trouvons sont probables, alors les résultats que nous trouverions par un calcul plus précis le seraient davantage.
Pourquoi est-il nécessaire de faire une simplification ? Simplement parce que nous aurions de très nombreux calculs à fournir pour chaque tableau ; nous aurions besoin de concepts mathématiques nettement plus compliqués. Nous allons montrer qu'avec des mathématiques simples, il est possible de démontrer le résultat attendu.
La simplification consiste à ne pas compter parmi tous les tableaux ceux qui sont des glissements horizontaux les uns des autres. Nous ne compterons parmi l'ensemble qu'un seul d'entre eux, celui qui contient le plus de positions.
En fait, entre deux tableaux qui sont des glissements horizontaux l'un de l'autre, il y a énormément de positions qui se recoupent, et c'est un très grand travail de savoir lesquels ne se recoupent pas (d'autant plus qu'il n'y en a pas beaucoup).
Il est donc inutile de mettre en _uvre des techniques difficiles pour obtenir des résultats à peine supérieurs.
Réduction verticale d'un tableau
Difficulté mathématique moyenne
Verticalisation
Pour parvenir à la meilleure estimation possible, il faut déterminer, parmi tous les tableaux de même impression qui sont des glissements l'un de l'autre, lequel contient le plus de positions ? Et bien, c'est tout simplement celui dont la distance de recherche est la plus grande.
Afin de bien comprendre ce principe, ayons en tête la notion de "longueur maximale de recherche" qui doit rester constante dans un tableau. On peut trouver cette notion dans le paragraphe : le critère de comparaison des tableaux. On peut constater que, pour des tableaux de même impression, plus le mot principal est oblique (plus le glissement horizontal est important), plus la place qu'il occupe est grande et plus la distance de recherche est forcément petite. Les deux paramètres varient dans un sens opposé ; cela est nécessaire pour que l'impression reste identique. Pour que des tableaux conservent la même impression lorsque la taille du mot principal s'allonge, la distance de recherche doit diminuer. Et de même lorsque la taille du mot principal se rétracte, le distance de recherche doit s'allonger.
Or il faut constater que pour une longueur maximale de recherche constante, plus la surface est compacte (ronde), plus elle est importante. La surface est donc maximale lorsque le mot principal est le plus réduit possible, c'est-à-dire lorsqu'il est placé le plus verticalement possible. C'est une constatation naturelle que nous ne démontrerons pas : un objet plus rond possède plus de surface qu'un objet plus allongé lorsqu'ils ont une même hauteur.
A partir de cette simplification, nous allons établir une estimation des positions. Lorsqu'un mot principal ne sera pas vertical, nous le ramènerons au maximum à la verticale par le procédé du glissement horizontal. Pour faire une simplification uniforme, nous supposerons que le mot principal peut être ramené entièrement à la verticale dans tous les tableaux. Bien que cela ne soit pas toujours possible (lorsque le code du mot principal n'est pas divisible par le nombre de glissement vertical, il n'est pas possible de ramené le tableau à la verticale). On pourrait penser que cela conduit à une surestimation. Mais il n'en est rien car - vu le nombre important de positions qui ne sont pas comptées en négligeant les tableaux obliques - le petit gain de surface apporté par la verticalisation d'un tableau dans les cas impossibles est vraiment négligeable. Quels que soient les tableaux, les comptes effectués seront une sous-évaluation du nombre de positions possibles.
Réduction
Nous effectuerons les calculs uniquement sur les tableaux où le mot principal est vertical, car cela simplifie les calculs. Le mot principal peut non seulement être disposé verticalement tout en conservant la même impression, mais il peut aussi subir une réduction verticale de telle sorte qu'il occupe une place minimale. Ce tableau particulier dont le mot principal occupe le minimum de place, nous lui donnerons le nom de tableau verticalisé-réduit. Evidemment dès qu'on transforme un tableau, il est nécessaire de changer la distance de recherche pour conserver la même impression.
Pour nous aider à comprendre cette verticalisation et cette réduction, voici un exemple de tableau qu'on pourrait avoir à étudier. Supposons de plus que la distance de recherche sur ce tableau est 1.5 :

Le tableau verticalisé-réduit est le tableau où le mot 'grand' apparaît verticalement avec des lettres consécutives. Et pour conserver la même impression selon le critère que nous avons posé, il faut calculer la distance de recherche du tableau verticalisé-réduit. Pour calculer cette distance, il suffit de procéder par la méthode suivante : La taille qu'occupe un mot verticalisé-réduit est très facile à déterminer à partir du nombre de lettres du mot : elle est égale au nombre de lettres du mot moins 1. Appelons V cette taille (dans notre exemple V = 4). Soit g la taille du glissement horizontal : c'est le nombre de glissements horizontaux entre deux lettres consécutives du mot (dans notre exemple g = 3). Et soit b le nombre de glissements verticaux (b=2). Par le théorème de Pythagore, on trouve que le mot oblique initial occupe la place suivante : V x Racine(g²+b²) . Lorsqu'on verticalise et qu'on réduit le tableau ci-dessus, on obtient le nouveau tableau suivant où la distance de recherche est environ 6.7.
Dans le tableau initial appelons la distance de recherche d (dans notre exemple d=1.5). Pour construire le tableau verticalisé-réduit offrant la même impression que ce tableau oblique initial, on commence par réduire et par verticaliser le tableau en choisissant la bonne largeur de tableau (réelle, et non apparente).
C'est ce que nous avons construit dans le tableau suivant:

Il faut ensuite calculer quelle doit être la nouvelle distance de recherche d' afin de conserver la même impression. D'après la règle de comparaison des tableaux que nous avons établie, il faut que la longueur maximale de recherche reste constante. Or la longueur maximale de recherche pour chacun des tableaux, c'est la somme de la place qu'occupe le mot principal augmentée de deux fois la distance de recherche. L'égalité qui permet de conserver la même longueur maximale de recherche s'écrit donc :
![]()
En transformant cette expression, on en déduit que :
La nouvelle distance de recherche d' lorsque le mot principal est verticalisé et réduit est
![]()
Où :
- d est la distance de recherche pour le tableau d'origine.
- V est la longueur qu'occupe le mot principal vertical, c'est le nombre de lettres du mot moins 1.
- g est le nombre de glissements horizontaux entre deux lettres consécutives dans le mot original.
- b est le nombre de lignes qu'il faut compter vers le bas d'une lettre à l'autre dans le mot original.
Ce tableau verticalisé-réduit est le tableau le plus compact qu'on puisse construire à partir du mot principal tout en conservant la même impression.
Etirement maximal
Difficulté mathématique moyenne
Nous avons vu que nous nous intéresserons uniquement aux tableaux dont le mot principal est vertical, car cela facilite les calculs. Nous cherchons à déterminer tous les tableaux (identiquement impressionnants au tableau initial) qui offrent de nouvelles positions possibles. Pour les trouver, il faut commencer par construire le tableau le plus compact (le tableau verticalisé-réduit). Les autres tableaux qui nous intéressent proviendront de ce tableau verticalisé-réduit par glissements verticaux. Une question naturelle se pose alors : jusqu'à combien de glissements verticaux peut-on étirer le mot tout en conservant un tableau qui soit identiquement impressionnant ? C'est-à-dire : combien de lignes peut-on sauter au maximum ? En disposant de cette réponse, nous connaîtrons tous les tableaux verticaux possibles ayant la même impression que celui de départ. Or la réponse s'impose pratiquement d'elle-même : on arrête d'étirer le tableau lorsque celui-ci devient trop étroit pour construire de nouvelles positions.
En terme mathématique, il faut que la distance de recherche d'' du tableau étiré au maximum vérifie d'' ³ 1. Cela signifie qu'on veut un tableau ayant au moins une distance de recherche de 1. Sous cette condition, on peut voir que l'étirement maximal a lieu quand d'' s'approche au maximum de 1. Ce choix de la valeur 1 est raisonnable car les lettres sont au minimum à la distance 1 les unes des autres. Ainsi nous sommes sûrs d'avoir des lettres à l'intérieur de la distance de recherche. Une valeur minimale de 0.5 aurait aussi été acceptable, mais pour se donner une certaine marge, nous nous contenterons de la valeur 1.
Le choix étant fait, calculons le nombre maximal de glissements : on se sert de d', c'est-à-dire la distance de recherche du tableau verticalisé-réduit. Appelons n le nombre de glissements verticaux maximum qu'on recherche.
Pour trouver la valeur de n, il suffit
d'écrire la règle de même impression en calculant la longueur maximale de recherche
pour le tableau verticalisé-réduit et pour le tableau étiré au maximum. Comme
d'' =1, on obtient l'égalité suivante : ![]() où V est la place qu'occupe le mot principal dans le tableau verticalisé-réduit.
On en déduit la formule suivante :
où V est la place qu'occupe le mot principal dans le tableau verticalisé-réduit.
On en déduit la formule suivante :
Le nombre maximal de glissements verticaux est :
![]()
Où :
- V est la taille du mot principal lorsqu'il est vertical et réduit.
- d' est la distance de recherche lorsque le mot principal est vertical et réduit
- la notation Ent[ ] signifie qu'on prend la partie entière (le plus petit nombre entier inférieur) de ce qui est entre crochet. En effet un résultat de 4.7 devra être arrondi à 4 car il n'est pas possible de sauter des demi-lignes
Une valeur de n = 1 signifierait qu'il n'est pas possible de construire d'autres tableaux que le tableau verticalisé-réduit tout en voulant conserver une impression semblable au tableau original.
En prenant la partie entière, nous faisons encore une sous-évaluation des résultats. Il ne faut tout de même pas penser que les résultats que nous obtiendrons sont très loin des résultats exacts, car les sous-évaluations ne sont pas grossières. Elles concernent toujours une petite partie du résultat. Nous pouvons penser que nos résultats seront très probablement inférieurs aux résultats réels, mais qu'ils seront tout de même assez significatifs de la réalité.
Si des résultats sous-évalués affirment que les tableaux sont normaux, alors des résultats précis affirmeraient d'autant plus la chose. Il n'est donc pas gênant de procédé à des petites simplifications qui finalement ne gêneront pas la démonstration.
Les glissements verticaux
Difficulté mathématique moyenne
Nous venons de calculer le nombre de glissements verticaux maximal. Cela signifie que pour un mot principal donné, on peut définir tous les tableaux verticaux qui lui sont identiquement impressionnants.
Nous allons étudier ces glissements verticaux plus en détail afin de déterminer le nombre total de positions que peut prendre un mot satellite dans tous les tableaux d'impression semblable. La tâche n'est pas des plus faciles ; c'est peut-être une des explications les plus difficiles de notre exposé. Il faudra être bien attentif.
Nous allons travailler sur un exemple. Pour tout tableau où apparaît un mot principal et un mot satellite, nous savons déterminer la distance de recherche en mesurant la distance entre le mot principal et le mot satellite. Dans le tableau suivant, qui nous servira d'exemple, le mot principal est 'mots' et le mot satellite est 'ici'. On calcule que la distance de recherche est égale à 3.6.
Voici le tableau initial qui est une tranche d'un tableau de 1801 lettres de large :

Comme nous l'avons vu, l'ensemble des tableaux où l'on va compter les positions possibles sont les tableaux verticaux. Si l'on en fait le décompte, ils commencent par le tableau verticalisé-réduit et finissent par le tableau de glissement vertical maximal.
Pour construire le tableau verticalisé il suffit de fabriquer le tableau de largeur 3600 et de prendre la partie où apparaît le mot principal. C'est ce que nous avons fait ci-dessous. En connaissant la distance de recherche du tableau oblique initial qui est d'environ 3.6, nous pouvons construire le tableau verticalisé-réduit dont la distance de recherche d' se calcule par une formule que nous avons établie avant. Le résultat est 6.3
Voici le tableau verticalisé-réduit (largeur du tableau 3600) ; on a dessiné chaque lettre sur un fond gris :

Par la formule que nous avons construite, nous pouvons déterminer que le nombre de glissements verticaux maximal est de 4. Voici donc les différents tableaux verticaux qu'on peut construire par le procédé du saut de lignes :
Le tableau correspondant à 2 glissements verticaux (largeur du tableau : 1800). Afin de reconnaître les lettres présentes dans le tableau verticalisé-réduit, on les a placées sur un fond gris. Les autres lettres sont de nouvelles lettres qui proviennent de la réduction de largeur du tableau de 3600 à 1800 :

Le tableau correspondant à 3 glissements verticaux (largeur du tableau : 1200) Afin de reconnaître les lettres présentes dans le tableau verticalisé-réduit, on les a placées sur un fond gris. Les autres lettres sont de nouvelles lettres qui proviennent de la réduction de largeur du tableau de 3600 à 1200 :

Le tableau correspondant à 4 glissements verticaux (largeur du tableau : 900). Afin de reconnaître les lettres présentes dans le tableau verticalisé-réduit, on les a placées sur un fond gris foncé. On peut aussi voir sur fond gris clair les lettres qui sont apparues dans le tableau à 2 glissements verticaux. Les autres lettres (une ligne sur 2) sont de nouvelles lettres qui proviennent de la réduction de largeur du tableau de 3600 à 900.
Et l'on s'aperçoit que c'est bien le dernier tableau possible :

Cet exemple est instructif pour tirer des leçons : en observant, on peut généraliser que dans un tableau à b glissements verticaux, on a b-1 lignes sur b qui sont faites de lettres nouvelles qui n'étaient pas dans le tableau verticalisé-réduit. En fait, ce n'est pas exactement b-1 lignes sur b qui sont nouvelles, il y a une petite fluctuation possible due à la position des bords. Mais en moyenne, ce résultat est exact. De plus, pour une distance de recherche assez grande, une telle approximation est même précise. Nous adopterons donc le fait que, dans un tableau à b glissements verticaux, 1 ligne sur b était présente dans le tableau verticalisé-réduit.
On peut voir que dans le tableau à 4 glissements verticaux, on retrouve le tableau à 2 glissements verticaux, 1 ligne sur 2 (les lignes grises ainsi que les lignes gris clair). Cela vient du fait que 4 est un multiple de 2. Plus généralement à chaque fois qu'on a deux tableaux dont les glissements verticaux ont un diviseur commun, il existe des lignes communes dans les tableaux.
Le décompte des positions possibles
Difficulté mathématique un peu plus élevée
Nous désirons connaître le nombre total de positions possibles pouvant être recensées dans tous les tableaux d'impression semblable. Il faut compter les positions dans le tableau verticalisé-réduit, puis dans le tableau à 2, à 3, et enfin à 4 glissements verticaux. Dans d'autres situations, on peut aller encore plus loin. Pour compter toutes les positions différentes, il faut procéder méthodiquement.
Exemple des deux premiers tableaux
On peut en effet remarquer que beaucoup de positions se retrouvent dans les différents tableaux.
Pour compter toutes les positions, il faut commencer par compter les positions du tableau verticalisé-réduit. Pour faire cela, nous avons une formule qui estime les positions en fonction de la surface de recherche (pour retrouver la formule, on pourra se reporter au paragraphe : "Le nombre de positions possibles pour le second mot").
Ensuite il faut compter les positions du tableau à 2 glissements verticaux. Le nombre de positions possibles dans ce tableau s'obtient par la même formule. Seulement, si on ajoute ces positions aux précédentes, il y a beaucoup de positions qui seraient comptées deux fois car beaucoup de positions du tableau à 2 glissements sont aussi présentes dans le tableau verticalisé-réduit.
La question importante est alors : combien y a-t-il de positions communes aux deux tableaux ? Et bien, il suffit de réaliser qu'une position du tableau à 2 glissements est aussi présente dans le tableau verticalisé-réduit seulement si elle n'est faite qu'à partir de lettres sur fond gris. Dès qu'une position contient une lettre nouvelle (sur fond blanc), c'est une position qui n'est pas dans le tableau verticalisé-réduit (et réciproquement, toute position faite uniquement de lettres grises est aussi dans le tableau verticalisé-réduit). Pour calculer le nombre de positions communes aux deux tableaux, nous allons construire un tableau particulier : nous allons extraire du tableau à 2 glissements uniquement les lettres présentes dans le tableau verticalisé-réduit. On obtient le tableau suivant qu'on appellera P2(2), le 2 en indice pour dire qu'on travaille sur le tableau à 2 glissements verticaux, et le 2 entre parenthèses pour dire que la surface ne prend en compte qu'une ligne sur deux du tableau cité.

Bien que ce tableau contienne les mêmes lettres que le tableau verticalisé-réduit, il en diffère par deux points :
- La largeur de la surface de recherche n'est pas la même que celle du tableau verticalisé- réduit ; c'est exactement celle du tableau à 2 glissements.
- La hauteur de recherche (la longueur maximale de recherche) est divisée par 2. En effet, tous les tableaux que nous avions construits avaient la même hauteur (pour respecter le principe de même impression). En prenant 1 ligne sur 2 dans le tableau à 2 glissements, on obtient approximativement la hauteur divisée par 2 ; ce qui conduit à une surface valant environ la moitié de la surface de recherche du tableau à 2 glissements. Dans un souci de simplification, nous considérerons que la surface est vraiment divisée par 2, car l'approximation est bonne dans la moyenne des situations (ainsi les petites erreurs se compenseront les unes avec les autres). Cette simplification nous permettra de calculer plus facilement la surface de ce tableau.
Le nombre de positions possibles dans ce tableau nous donnera les positions communes au tableau verticalisé-réduit et au tableau à 2 glissements. Or le nombre de positions est estimé au moyen des surfaces comme nous l'avons déjà vu dans le chapitre : "Le nombre de positions possibles pour le second mot".
Nous n'allons pas reconstruire ici le même raisonnement que nous avions élaboré dans ce chapitre car c'est exactement la même construction. La seule différence ici est que toutes les hauteurs des surfaces mises en jeu sont divisées par 2. Il suffit de reconstruire la formule que nous avions trouvée en la modifiant très légèrement : il faut diviser par 2 toutes les surfaces. On obtient ainsi la formule suivante :
Nombre de positions communes =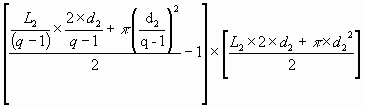
Ce qui donne le résultat suivant lorsqu'on simplifie :
Nombre de positions communes =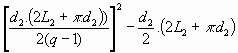
Où d2 et L2 sont la distance de recherche et la taille du mot principal dans le tableau étiré à 2 glissements. Le nombre de positions du tableau P2(2), comme le tableau lui-même, sera aussi noté P2(2) de la même façon afin de faciliter la terminologie.
Seulement, il faut pouvoir déterminer L2 et d2 :
- Si on appelle V la taille du mot principal verticalisé-réduit, alors L2 = 2V.
- Pour trouver d2, qui est la distance de recherche du tableau à 2 glissements verticaux, il suffit de poser la règle de même impression : si on appelle d la distance de recherche du tableau verticalisé-réduit, il faut que V+2d=2V+2d2. On obtient alors que d2=d -V/2 .
On peut ainsi procéder au calcul des positions communes dans l'exemple ci-dessus avec un mot satellite de 3 lettres : d2=2 et L2=6, d'où P2(2)=76.4. C'est le nombre de positions communes aux deux premiers tableaux.
Pour comptabiliser le nombre total de positions différentes des deux premiers tableaux, il faut faire la somme des positions de chacun des tableaux, puis retirer les 76.4 positions que l'on compte deux fois.
Il faudra reproduire cette même méthode pour chaque nouveau tableau. C'est ainsi que l'on construit une méthode pour le cas général :
- Commençons par calculer la distance de recherche d'un tableau à n glissements verticaux. Si V est la longueur qu'occupe le mot verticalisé-réduit - c'est-à-dire le nombre de lettres du mot principal moins 1 - et si d est la distance de recherche pour ce mot vertical, alors le mot principal du tableau à n glissements verticaux occupera tout simplement la taille V.n.
Il faut remarquer qu'il n'est pas toujours possible d'effectuer n glissements verticaux. En effet, un glissement vertical se construit en réduisant la largeur réelle du tableau. Si la taille du Code Secret n'est pas divisible par n, il n'est pas possible d'imposer que le tableau avec n glissements soit vertical ; dans ce cas, si l'on cherche à sauter n lignes, le mot principal est forcément oblique. Nous ferons nos calculs comme si nous pouvions toujours supposer le mot principal vertical. Cette supposition ne modifie pas sensiblement les résultats, qui sont par ailleurs sous-évalués.
Ainsi pour trouver la nouvelle distance de recherche dn d'un tableau à n glissements, il suffit de vérifier la condition de même impression à partir du tableau verticalisé-réduit : V.n+2dn=V+2d ; on obtient que :
La distance dn de recherche pour un tableau à n glissements verticaux est :
![]()
Où :
- d est la distance de recherche du tableau verticalisé-réduit
- V est la taille du mot principal dans le tableau verticalisé-réduit (c'est le nombre de lettres moins 1)
- Déterminons ensuite une formule générale qui permet de calculer les positions communes à deux tableaux. La formule est analogue à celle que nous avons construite pour les deux premiers tableaux.
Nous avons vu que toute la méthode réside dans la construction du tableau P2(2) qui contient l'ensemble des positions communes aux deux tableaux. De la même façon nous allons construire un tableau que nous appellerons Pn(z) qui permettra de compter les positions communes. Pn(z) est le tableau construit de la façon suivante : à partir du tableau à n glissements, on ne prend en compte que une ligne sur z ; ceci donne un tableau de même largeur que le tableau à n glissements, mais avec une hauteur divisée par z. Nous considérerons que la surface entre le tableau à n glissements et Pn(z) est rigoureusement divisée par z, même si ce n'est pas toujours exactement le cas comme nous l'avons vu pour P2(2). Mais comme nous l'avons dit cette estimation est une bonne approximation.
Nous appellerons aussi Pn(z) le nombre de positions qu'on peut construire dans ce tableau.
Par la même technique que précédemment, on obtient la formule suivante :
Le nombre de positions du tableau Pn(z) à n glissements où l'on ne retient que 1 ligne sur z est :
Pn(z)
=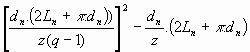
Où :
- q est le nombre de lettres du mot satellite.
- Ln est la longueur qu'occupe le mot principal vertical dans le tableau à n glissements verticaux.
- dn est la distance de recherche dans le tableau à n glissements verticaux.
La formule que nous venons d'établir permet de calculer les positions du mot satellite pour de nombreux types de tableaux. Il faut maintenant étudier comment utiliser cette formule pour comptabiliser toutes les positions possibles.
En remarque préliminaire, rappelons que nous utilisons la même notation Pn(z) pour parler deux choses distinctes : tout d'abord pour le nombre de positions possibles à l'intérieur du tableau à n glissements où l'on ne retient que 1 ligne sur z, mais aussi pour le tableau lui-même.
En seconde remarque, il faut bien comprendre que tous ces calculs que nous proposons supposent que le mot principal ait un code secret assez large afin de pouvoir procéder à suffisamment de glissements verticaux en ayant toujours assez de nouvelles lettres disponibles. Ils supposent qu'il y a toujours assez de lettre pou former n'importe quel tableau, ce qui n'est en réalité pas toujours vrai. Mais nous intégrerons dans notre modèle cette supposition que la taille du code est assez large, qu'il y a toujours assez de lettres pour fabriquer tous les tableaux. Ceci semble introduire une majoration de l'estimation lorsque le code du mot principal est petit, ou bien lorsqu'on se trouve avec un code important aux limites du texte. En fait, la quasi-totalité des tableaux que nous allons étudier ne présentent pas cet inconvénient, car la suppositon est confirmée en pratique (le code est assez grand relativement à la distance de recherche des mots satellites et le tableau se trouve assez loin des limites du texte); et pour ceux qui le présenteraient, nous ne constaterions pas une grande erreur d'estimation. Le modèle est donc très intéressant, car malgré la complexité du problème abordé, la résolution restera relativement simple.
Ces préliminaires importants étant faits, procédons à la synthèse de l'estimation du nombre de positions. Pour faire le compte précis des positions d'un tableau quelconque, il faut utiliser une méthode de décompte très rigoureuse, afin de ne pas en oublier et de ne pas en compter en trop non plus:
· La première étape consiste à compter les positions du tableau verticalisé-réduit. Selon les notations que nous avons choisies, ce nombre de position se note P1(1) et se calcule à partir de la formule générale que nous avons établie.
· Il faut ensuite déterminer le nombre de positions du tableau à 2 glissements verticaux, on le note P2(1). Pour compter les positions données par P2(1), il faut calculer d2 par la formule appropriée (il ne faudra pas oublier de faire de même pour chaque glissement différent). Et maintenant il faut bien penser à retirer les positions de ce tableau qui sont communes avec le tableau verticalisé-réduit, P1(1). Ces positions sont comptées dans P2(2). Si l'on fait le compte des positions nouvelles apportées par le tableau P2(1), le nombre s'élève à P2(1)-P2(2).
· Puis on compte les positions du tableau à 3 glissements verticaux, c'est P3(1). Il faut retirer les positions qu'on a déjà comptées dans les tableaux P1(1) et P2(1). On peut remarquer que les positions communes à P3(1) et P1(1) sont données par P3(3). On peut aussi remarquer qu'il n'y a pas de positions spécifiques à P2(1) qui soit dans P3(1) ; cela provient du fait que les nombres 2 et 3 n'ont pas de multiples communs, c'est pourquoi ces deux tableaux n'ont pas de lignes communes en dehors des lignes du tableau verticalisé-réduit. Les seules positions à soustraire sont donc P3(3). Si l'on fait le compte des positions nouvelles apportées par le tableau P3(1), le nombre s'élève à P3(1)-P3(3).
· Il faut ensuite ajouter les positions du tableau à 4 glissements verticaux, P4(1) ; tout en retirant les positions déjà comptées dans les tableaux précédents, de P1(1) à P3(1). Si nous observons l'exemple que nous avons donné où nous voyons le tableau à 4 glissements verticaux, on peut remarquer que les lignes qui ne sont pas nouvelles sont exactement celles du tableau P2(1). On en déduit que les positions qu'il faut ôter sont exactement les positions qui sont faites avec 1 ligne sur 2, soit P4(2). En regardant rapidement on pourrait croire que P4(2) est le même tableau que P2(1). Ce serait le cas si les distances de recherche étaient les mêmes. Mais en regardant de plus près, on s'aperçoit que le tableau P2(1) est plus large que P4(1) ; ce ne sont donc pas les mêmes tableaux. Les positions qui sont déjà comptées correspondent donc à P4(2). Si l'on fait le compte des positions nouvelles apportées par le tableau P4(1), le nombre s'élève à P4(1)-P4(2).
· Pour le tableau à 5 glissements verticaux, on procède comme pour P3(1). On obtient que le compte des positions nouvelles apportées par le tableau P5(1) s'élève à P5(1)-P5(5).
· Il faut ensuite compter les positions du tableau à 6 glissements verticaux (évidemment, il ne faut les compter que si le nombre de glissements verticaux maximal s'élève au moins jusque là). Ce nombre de positions est donné par P6(1). Il faut bien sûr retirer les positions déjà comptées dans les tableaux précédents de P1(1) à P5(1). En réfléchissant, on obtient que les positions qu'il faut ôter sont P6(2) et P6(3). En effet, dans P6(1) 1 ligne sur 2 fait partie de P2(1) et 1 ligne sur 3 fait partie de P3(1). En retirant P6(2) et P6(3), on a retiré toutes les positions déjà comptées parce que les positions de P6(4) sont déjà retirées dans P6(2), et parce que P6(5) n'a pas de positions spécifiquement communes avec les autres tableaux. Par contre, il faut être vigilant : en retirant P6(2) et P6(3), on a retirer deux fois les positions de P6(6). En effet, P6(6) est compté dans chacun des tableaux P6(2) et P6(3). Il faut donc rajouter P6(6) au compte final. Le total des positions nouvelles apportées par le tableau P6(1) s'élève donc à P6(1)- P6(2)- P6(3)+ P6(6).
Autant qu'un tableau nous permettra de sauter des lignes, il faudra continuer cet algorithme (aussi loin qu'il est nécessaire). Nous n'irons pas plus loin dans les explications pour les valeurs de n supérieures. Nous pourrons juste remarquer que pour un tableau Pn(1), les positions à retirer concernent uniquement les tableaux Pn(z), où z a un multiple commun avec n. Nous n'étudierons pas tous les cas en cherchant une formule générale un petit peu difficile, car très peu des tableaux étudiés nécessitent des valeurs de n élevées. Les calculs peuvent être effectués facilement à la main.
Voici le résumé des formules à utiliser pour compter les différentes positions nouvelles apportées par chaque nouveau tableau produit par un glissement vertical :
Positions nouvelles à ajouter pour chaque tableau à n glissements verticaux :
· Pour n=1 le nombre de positions nouvelles s'élève à P1(1)
· Pour n=2 le nombre de positions nouvelles s'élève à P2(1)- P2(2)
· Pour n=3 le nombre de positions nouvelles s'élève à P3(1)- P3(3)
· Pour n=4 le nombre de positions nouvelles s'élève à P4(1)- P4(2)
· Pour n=5 le nombre de positions nouvelles s'élève à P5(1)- P5(5)
· Pour n=6 le nombre de positions nouvelles s'élève à P6(1)- P6(2)- P6(3)+ P6(6)
· Pour n=7 le nombre de positions nouvelles s'élève à P7(1)- P7(7)
· Pour n=8 le nombre de positions nouvelles s'élève à P8(1)- P8(2)
· Pour n=9 le nombre de positions nouvelles s'élève à P9(1)- P9(3)
· Pour n=10 le nombre de positions nouvelles s'élève à P10(1)- P10(2)- P10(5)+ P10(10)
· Pour n=11 le nombre de positions nouvelles s'élève à P11(1)- P11(11)
· Pour n=12 le nombre de positions nouvelles s'élève à P12(1)- P12(2)- P12(3)+ P12(6)
· Pour n=13 le nombre de positions nouvelles s'élève à P13(1)- P13(13)
· Pour n=14 le nombre de positions nouvelles s'élève à P14(1)- P14(2)- P14(7)+ P14(14)
· Pour n=15 le nombre de positions nouvelles s'élève à P15(1)- P15(3)- P15(5)+ P15(15)
· Pour n=16 le nombre de positions nouvelles s'élève à P16(1)- P16(2)
· Etc...
Nous arrêterons là les comptes de positions car il y a aura probablement peu de tableaux atteignant de telles valeurs de glissements.
Avec ces formules, il est possible de calculer une estimation du nombre de positions totales que peut prendre un mot satellite autour d'un mot principal donné.
Lorsque nous effectuerons un calcul, il ne faudra évidemment ajouter les positions d'un tableau Pn(1) que si le glissement vertical maximal est au moins égal au cas concerné.
Un exemple de calcul
Difficulté mathématique moyenne
Au bout de cette étude, nous possédons le moyen d'estimer assez précisément le nombre de positions possibles qui permettent de faire apparaître deux mots dans la Torah.
Nous allons présenter un exemple qui résumera le calcul a effectuer pour obtenir le résultat recherché ;
Supposons que nous travaillions dans un texte de 305 000 lettres (c'est environ un livre de 200 bonnes pages). Celui-ci est écrit au hasard dans un alphabet de 22 lettres. On supposera que toutes les lettres apparaissent avec la même fréquence. Supposons que nous ayons trouvé le tableau ci-après à l'intérieur de ce texte. Nous désirons en mesurer l'espérance afin de savoir si ce tableau est extraordinaire ou non ?

- Premièrement nous pouvons calculer
l'espérance du mot principal. En vertu de la formule suivante :
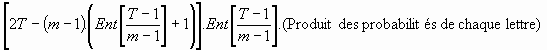
, le mot 'premier' possède une espérance d'apparition de :
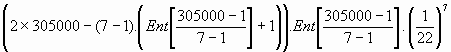 =
6.22.
=
6.22.
C'est le nombre moyen de fois qu'il apparaît dans un texte de 305 000 lettres ainsi composé.
- Observons maintenant le mot 'deux'.
Il est à la distance d =
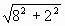
On en déduit la distance de recherche du tableau verticalisé-réduit par la formule suivante :
![]() ,
ainsi
,
ainsi ![]() =11.95
=11.95
- Le nombre de glissements verticaux maximal d'un tableau identiquement impressionnant est donné par la formule :
![]() d'où le résultat
d'où le résultat ![]() = 4.
Il faudra donc étudier tous les tableaux à glissements verticaux de 1 à 4.
= 4.
Il faudra donc étudier tous les tableaux à glissements verticaux de 1 à 4.
- D'après la formule générale de
Pn(z)=
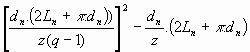
- Ajoutons les positions supplémentaires qui viennent du tableau à 2 glissements verticaux :
Calculons d'abord la distance de recherche dans P2(1), L2=12 et d2=8.96. Par la formule appropriée, on en déduit P2(1) » 23 800 auquel il faut ôter P2(2) » 5 800
- Puis pour P3(1), on a L3= 18 et d3=5.96. Il s'ensuit que P3(1) » 11 500, auquel il faut retirer P3(3) » 1 200
- Et enfin pour P4(1), on a L4= 12 et d4=8.96, On obtient que P4(1) » 3 000, auquel il faut retirer P4(2) » 700
- De tous ces résultats, on déduit
que l'estimation du nombre de position est d'environ 69 000. Ce qui nous
nous conduit à calculer l'espérance d'apparition par le calcul suivant :
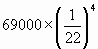
= 0.29 : c'est l'espérance de trouver le mot satellite près d'un mot principal choisi. Mais il faut penser qu'il y a probablement 6.21 fois le mot principal.
- D'où le résultat final : L'espérance de voir apparaître un tableau similaire à celui que nous avons présenté dans le texte est de 6.21x0.29=1.8. Cela signifie que ce genre de tableau peut se trouver 1.8 fois en moyenne dans les conditions citées ; ce qui est tout à fait probable.
|
Du même auteur : | ||||
| Connexion privée | Contact | Proposer de l'aide | Signaler un problème | Site philosophique flexe |