|
Mise en perspective du Théorème de Gödel
|
|
|
|
A partir d'un regard philosophique sur la nature des mathématiques, le theoreme de Gödel (...)
|
Etude du Code Secret de la Bible - Analyse détaillée
Annexe 2: Formulaire
Voici l'essentiel des formules qui permettent de procéder aux calculs évaluant la validité du Code Secret :
L'espérance de trouver un mot, à l'endroit ou à l'envers, dans un texte par le procédé du saut de lettre est donc :
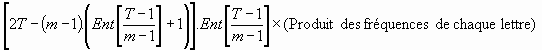
- m le nombre de lettre du mot cherché
- T la taille du texte
Le nombre de positions possibles pour trouver un mot satellite à proximité d'un mot principal dans un tableau donné est estimé par :
nombre de positions =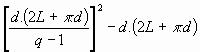
Où :
- d est la distance de recherche
- q est le nombre de lettres du mot satellite
- L est la taille qu'occupe le mot principal.
(l'unité étant la distance entre deux lettres consécutives)
La nouvelle distance de recherche d' lorsque le mot principal est verticalisé et réduit est
.
Où :
- d est la distance de recherche pour le tableau d'origine.
- V est la longueur qu'occupe le mot principal vertical, c'est le nombre de lettres du mot moins 1.
- g est le nombre de glissements horizontaux entre deux lettres consécutives dans le mot original.
- b est le nombre de lignes qu'il faut compter vers le bas d'une lettre à l'autre dans le mot original.
Le nombre maximal de glissements verticaux est :
Où :
- V est la taille du mot principal lorsqu'il est vertical et réduit.
- d' est la distance de recherche lorsque le mot principal est vertical et réduit
- la notation Ent[ ] signifie qu'on prend la partie entière (le plus petit nombre entier inférieur) de ce qui est entre crochet. En effet un résultat de 4.7 devra être arrondi à 4 car il n'est pas possible de sauter des demi-lignes
La distance dn de recherche pour un tableau à n glissements verticaux est :
Où :
- d est la distance de recherche du tableau verticalisé-réduit
- V est la taille du mot principal dans le tableau verticalisé-réduit (c'est le nombre de lettres moins 1)
Le nombre de positions du tableau Pn(z) à n glissements où l'on ne retient que 1 ligne sur z est :
Pn(z) =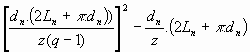
Où :
- q est le nombre de lettres du mot satellite.
- Ln est la longueur qu'occupe le mot principal vertical dans le tableau à n glissements verticaux.
- dn est la distance de recherche dans le tableau à n glissements verticaux.
Positions nouvelles à ajouter pour chaque tableau à n glissements verticaux :
- Pour n=1 le nombre de positions nouvelles s'élève à P1(1)
- Pour n=2 le nombre de positions nouvelles s'élève à P2(1)- P2(2)
- Pour n=3 le nombre de positions nouvelles s'élève à P3(1)- P3(3)
- Pour n=4 le nombre de positions nouvelles s'élève à P4(1)- P4(2)
- Pour n=5 le nombre de positions nouvelles s'élève à P5(1)- P5(5)
- Pour n=6 le nombre de positions nouvelles s'élève à P6(1)- P6(2)- P6(3)+ P6(6)
- Pour n=7 le nombre de positions nouvelles s'élève à P7(1)- P7(7)
- Pour n=8 le nombre de positions nouvelles s'élève à P8(1)- P8(2)
- Pour n=9 le nombre de positions nouvelles s'élève à P9(1)- P9(3)
- Pour n=10 le nombre de positions nouvelles s'élève à P10(1)- P10(2)- P10(5)+ P10(10)
- Pour n=11 le nombre de positions nouvelles s'élève à P11(1)- P11(11)
- Pour n=12 le nombre de positions nouvelles s'élève à P12(1)- P12(2)- P12(3)+ P12(6)
- Pour n=13 le nombre de positions nouvelles s'élève à P13(1)- P13(13)
- Pour n=14 le nombre de positions nouvelles s'élève à P14(1)- P14(2)- P14(7)+ P14(14)
- Pour n=15 le nombre de positions nouvelles s'élève à P15(1)- P15(3)- P15(5)+ P15(15)
- Pour n=16 le nombre de positions nouvelles s'élève à P16(1)- P16(2)
- Etc...
Le coefficient d'ajustement du nombre de positions pour un tableau à trois mots est :
A= 
Où :
- G est la surface de recherche autour du mot principal
- P est la surface de recherche autour du mot satellite
- C est la surface commune à G et P
- h est le gain moyen de surface pour des lettres de G et P.
On peut facilement calculer que h oscille entre 0 et 
.
On peut aussi s'apercevoir que plus C est grand, plus h est grand.
Pour le troisième mot d'un tableau :
- A, le coefficient d'ajustement varie entre 0.5 et 1.
- A est proche de 0.5 quand la partie commune C est presque réduite au néant et que les deux mots sont à peu près de la même longueur,
- A est proche de 1 quand la partie commune C avoisine la taille du petit mot, c'est-à-dire lorsque la partie commune est maximale.
Le nombre de positions pour un mot par rapport à un ensemble de mot est :
Nombre de positions = 
- F est la surface de recherche formée par l'ensemble des mots auprès desquels on cherche le nouveau mot.
- A est le coefficient d'ajustement,
- r est le nombre de lettres du mot dont on étudie l'espérance.
|
Du même auteur : | ||||
| Connexion privée | Contact | Proposer de l'aide | Signaler un problème | Site philosophique flexe |